数据结构 树

数据结构-树和二叉树

树，二叉树，二叉树的遍历

Posted by Hzy on November 21, 2019

1.什么是树？

    1. 树是一种非线性的储存结构，跟之前学的线性表不同.

1.1 树结构中的一些基本术语，看着图好理解。

网上拿来的图

  • 树节点：像A,B,C,D,E,F，G…..都是树的节点
  • 孩子节点，父节点：像A是B的父节点，B是A的孩子节点，是相对的。
  • 兄弟节点： 像B，C，D都是兄弟节点，因为他们有共同的父节点A
  • 节点层数，A为第一层，B,C,D为第二次，往下推，总共有4层，
  • 树的高度，同上，4层就代表了树的高度。
  • 森林:森林就是要有好几棵树，像在A中，有B,C,D这三棵树，就可以称为森林。

1.2 用代码模拟上图中的树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

class Node:
    def __init__(self,data,next):
        self.data = data
        self.next = next

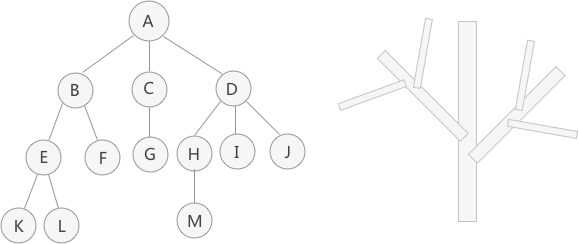
L = Node('L',None)
K = Node('K',None)
F = Node('F',None)
E = Node('E',[K,L])
B = Node('B',[E,F])
G = Node('G',None)
C = Node('C',[G])
M = Node('M',None)
H = Node('H',[M])
I = Node('I',None)
J = Node('J',None)
D = Node('D',[H,I,J])
A = Node('A',[B,C,D])

### 2. 二叉树:每个节点最多只有两个的树。

  • 在二叉树的第 i 层上至多有2i-1个结点 ，比如第一层只有1个节点，第二层有2个，第三层有4个，以此类推 8，16，32，64….
  • 深度为 k 的二叉树上至多含 2^k-1 个结点（k≥1）
  • 二叉树中储存结构分为顺序存储结构和链式储存结构

#### 2.1 二叉树中的顺序(数组)储存结构，只有完全二叉树能使用顺序存储结构，其他树得先转换成完全二叉树。

2.2 二叉树中的链式储存结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 定义一个节点，这里定义的节点只有左子树和有右子树，如果需要还可以加一个指向父节点的指针，称为三叉链表
class Node:
    def __init__(self,data):
        self.left = None
        self.data = data
        self.right = None
    def setLeft(self,left):
        self.left = left
        return self
    def setRight(self,right):
        self.right = right
        return self
'''
来模拟这棵树的存储
     1
    / \
   2   3
  /
  4
'''

def createTree():
    n4 = Node(4)
    n2 = Node(2).setLeft(n4)
    n3 =Node(3)
    n1 = Node(1).setLeft(n2).setRight(n3)
    return n1


t = createTree()
print(t.data)

2.3 二叉树的几种遍历方式

  • 先序遍历 根节点 -> 左子树 -> 右子树
  • 中序遍历 左子树 -> 根节点 -> 右子树
  • 后序遍历 左子树 -> 右子树 -> 根节点
  • 层次遍历 一层一层遍历二叉树，存储到数组中

2.4.1 先序遍历代码 递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

t = createTree()


# 先序遍历 递归版本

def printTree(tree,l):
    if tree:
        l.append(tree.data)
        printTree(tree.left,l)
        printTree(tree.right,l)
    return l

l = printTree(t,[])
print(l)

2.4.2 先序遍历代码 非递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 先序遍历，非递归版本，依靠栈来实现
def printTree1(tree):
    l = []
    stack = [tree]  # 根节点
    while stack:  # 当栈为空时，退出循环
        p = stack.pop()  # 弹出节点
        while p:
            l.append(p.data)  # 把节点中的值添加到列表中，打印
            if p.right:  # 如果节点有右子树，压入栈
                stack.append(p.right)
            p = p.left  # 节点一直指向左子树
    return l


print(printTree1(t))

2.5.1 中序遍历代码 递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

t = createTree()


# 中序序遍历 递归版本

def printTree(tree,l):
    if tree:
        printTree(tree.left, l)
        l.append(tree.data)
        printTree(tree.right, l)

    return l

l = printTree(t,[])
print(l)

2.5.2 中序遍历代码 非递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 中序遍历，非递归版本，依靠栈来实现
def printTree1(tree):
    l = []
    p = tree
    stack = []  # 栈
    while stack or p:  # 当栈为空时，退出循环
        if p:
            stack.append(p)
            p = p.left
        else:
            p = stack.pop()
            l.append(p.data)
            p = p.right

    return l

print(printTree1(t))

2.6.1 后序遍历 递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14

t = createTree()


# 后序序遍历 递归版本

def printTree(tree,l):
    if tree:
        printTree(tree.right, l)
        l.append(tree.data)
        printTree(tree.left, l)
    return l

l = printTree(t,[])
print(l)

2.6.2 后序遍历 非递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 后序遍历，非递归版本，依靠栈来实现
def printTree1(tree):
    l = []
    p = tree
    stack = []  # 栈
    while stack or p:  # 当栈为空时，退出循环
        if p:  # 入栈，同时继续指向右子树
            stack.append(p)
            p = p.right
        else:  # 出栈，打印，节点指向左子树
            p = stack.pop()
            l.append(p.data)
            p = p.left

    return l


print(printTree1(t))

2.7.1 层序遍历

  • 利用队列的特性，首先根节点入队，然后出队的同时，将其左右子树，入队，循环进行此操作，知道队列为空！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 层序遍历,利用队列的特性
def printTree(tree):
    t = tree
    l = []
    queue = []
    queue.append(t) # 先将跟节点入队
    while queue: # 队列不为空
        node = queue.pop(0)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)

        l.append(node.data)

    return l
print(printTree(t))
FEATURED TAGS
Python 数据结构